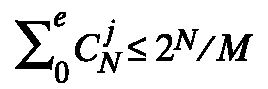Ричард Уэсли Хемминг (11 февраля 1915, Чикаго, штат Иллинойс - 7 января 1998, Монтеррей, Калифорния)

В книге Стефана Цвейга “Звездные часы человечества” есть замечательный рассказ “Гений одной ночи” об офицере французской армии Руже де Лиле, написавшем в течение одной ночи в пылу охватившего его вдохновения знаменитую “Марсельезу”. Это было в 1792 в революционном Марселе. Песня в течение нескольких дней распространилась по Франции, быстро приобрела колоссальную популярность во всём мире и впоследствии стала национальным гимном Французской республики. История сохранила имя Руже в памяти потомства благодаря этой единственной песне.

По аналогии Ричарда Хэмминга можно назвать “гением одной идеи”. Он сформулировал ее в 1950 в своей единственной научной статье, посвящённой кодам для коррекции ошибок. Статья содержала конструкцию блочного кода, корректирующего одиночные ошибки, которые возникают при передаче сообщений.

Ричард Хэмминг постоянно вёл активные научные исследования, однако знаменитой стала его единственная работа в области теории информации, составляющая по своему объему ничтожный процент его научного творчества. Эта статья быстро получила мировую известность и принесла ему заслуженную славу.

Подобно тому, как вслед за открытиями Фарадея и Максвелла последовали многочисленные изобретения в области электросвязи, изменившие нашу жизнь, так и после создания Клодом Шенноном теории информации и Владимиром Котельниковым теории потенциальной помехоустойчивости открылись новые возможности для развития телекоммуникаций. Одним из важнейших разделов теории информации является теория кодирования, основы которой были заложены Хэммингом.

Шеннон установил, что по каналу связи информация может передаваться безошибочно в том случае, если скорость передачи не превышает его пропускной способности. Однако доказательство Шеннона носило неконструктивный характер. Более поздние его исследования и другого американского ученого С. О. Райса показали, что практически любой случайно выбранный код позволяет достичь теоретического предела помехоустойчивости приёма сообщений. Однако такой код имел высокую сложность декодирования: число операций, необходимых для декодирования принятой кодовой комбинации, возрастал экспоненциально росту его длины.

Хэмминг был первым, кто предложил конструктивный метод построения кодов с избыточностью и простым декодированием. Его труд предопределил направление большинства работ в этой области, последовавших позже.

В 1937 он окончил Чикагский университет и получил степень бакалавра. Он продолжил образование в университете штата Небраска, где в 1939 ему была присвоена следующая – магистерская степень. В 1942 Ричард стал доктором философии в области математики в университете штата Иллинойс.

В 1945 Хэмминг участвовал в знаменитом Манхэттенском исследовательском проекте, целью которого было создание атомной бомбы.

А с 1946 в лаборатории Белла он начинает заниматься конструированием компьютеров. В этом знаменитом центре, где трудились К. Шеннон и многие другие выдающиеся учёные, ему суждено было проработать почти тридцать лет.

В 1976 Ричард переезжает в город Монтеррей (штат Калифорния) и возглавляет научные исследования в области вычислительной техники в Высшем военно-морском училище. В этом училище он преподавал и писал книги по теории вероятностей и комбинаторике.

Пионерская работа Хэмминга была отмечена многими наградами. В 1968 он стал почётным членом Института инженеров по электротехнике и электронике (IEEE) и был награждён премией Тьюринга Ассоциации компьютерных технологий. За исключительный вклад в развитие информационных наук и систем в 1979 ему присуждена премия Эммануила Пиоре. В 1980 его избрали членом Национальной Академии инженерных наук, в 1981 он получил премию Гарольда Пендера от Пенсильванского университета, а в 1988 – почётную медаль IEEE. В 1996 в Мюнхене за работу по кодам, корректирующим ошибки, Хэмминг был удостоен престижной премии Эдуарда Рейма в размере $130 000.

В его честь Институт инженеров по электротехнике и электронике учредил медаль, которой награждаются ученые, внесшие значительный вклад в теорию информации.

Коды, способные корректировать ошибки (в каналах связи в цифровых вычислительных машинах и т. п.) при обработке сигналов, были предложены Хэммингом ещё до 1948, когда была опубликована знаменитая статья Шеннона “Математическая теория связи”, заложившая прочную основу теории в данной области.

В этой статье Шеннон, ссылаясь на исследование, выполненное в 1947 его сослуживцем по лаборатории Белла Ричардом Хэммингом, описал в качестве примера простой код длины 7, корректирующий все одиночные ошибки. Публикация же оригинального материала Хэмминга по патентным соображениям была задержана до апреля 1950. Следует отметить, что пример корректирующего ошибки кода, приведенный в упомянутой статье Шеннона, инициировал исследование другого американского учёного, М. Е. Голея. Голей независимо от Хэмминга открыл коды, корректирующие одиночные ошибки. В 1949  (т. е. раньше Хэмминга) он опубликовал короткую заметку (всего на полстраницы) о своих результатах в Трудах IЕЕE. В этой заметке он рассмотрел не только бинарные коды, но и коды общего вида, комбинации которых принадлежат конечному полю (математическому множеству элементов с определенными операциями сложения, вычитания, деления и умножения) с рⁿ элементами (р – простое, а n – целое число).

Надо отметить, что ряд основополагающих идей теории связи был известен в качестве частных математических результатов ещё до того, как их начали применять учёные, решающие проблемы передачи сообщений по каналам связи. В своей книге “Алгебраическая теория кодирования” крупный американский специалист в области теории кодирования Э. Берлекамп сделал весьма интересное замечание. Он отметил, что конструкция кодов Хэмминга была описана в ином контексте ещё в 1942 г. известным американским математиком Р. А. Фишером, в работе посвященной теории факторного анализа (одного из разделов математической статистики) и её связи с математической теорией групп. Кстати, теорема В. А. Котельникова, указывающая на возможность представления аналоговых сигналов в цифровом виде, тоже была открыта как один из частных математических результатов теории интерполяции функции ещё в начале ХХ века английскими математиками Е. Т. и Дж. М. Уиткерами. Следует подчеркнуть, что ни Фишер, ни упомянутые английские ученые не связывали свои результаты с важнейшими для современного мира проблемами передачи информации по каналам связи.

Вольфганг Гёте говорил: “Недостаточно только получить знание; надо найти ему приложение. Недостаточно только желать; надо делать”. Для теории и техники связи теорема Котельникова и коды Хэмминга имеют исключительное значение, поскольку именно благодаря им перед инженерами открылась ясная перспектива создания цифровых систем, которые в конце ХХ века произвели революцию в электросвязи и поэтому их с полным основанием называют именами этих учёных.

Став катализатором, ускорившим развитие теории кодирования, статья Хэмминга обратила на себя внимание научной общественности. Во всех учебниках этот класс кодов называют кодами Хэмминга и изложение теории кодирования начинают с описания их конструкции. По-видимому, всё же было бы справедливее эти коды называть кодами Хэмминга – Голея, учитывая, что Голей пришёл к тем же идеям, что и Хэмминг, независимо и опубликовал их раньше. То, что его статья не вызвала к себе должного внимания, скорее всего, является волей случая.

По сравнению с теорией Шеннона коды, введенные Хэммингом, были разочаровывающе слабы. Однако предложенные Хэммингом регулярные методы построения кодов, корректирующих ошибки, имели фундаментальное значение. Они продемонстрировали инженерам практическую возможность достижения тех пределов, на которую указывали законы теории информации. Эти коды нашли практическое применение при создании компьютерных систем. Статья Хэмминга привела также к решению проблемы более плотной упаковки для конечных полей. Он ввел в научный обиход важнейшие понятия теории кодирования – расстояние Хэмминга между кодовыми комбинациями в векторном пространстве, определяемом для двоичных кодов как количество позиций этих комбинаций с различными символами, и границы Хэмминга для исправляющей способности блочных корректирующих кодов. Граница Хэмминга для двоичных кодов рассчитывается по следующей формуле:

В этом выражении число ошибок e может быть исправлено корректирующим блочным кодом длиной N, имеющим М кодовых комбинаций (C^j_N – биномиальный коэффициент).

Работа Хэмминга сыграла ключевую роль в последующем развитии теории кодирования и стимулировала обширные исследования, выполненные в последующие годы. В 1956 г. Давид Слепян первым изложил теорию кодов с проверкой четности на серьезной математической основе. Главный сдвиг в области теории кодирования произошел, когда французский ученый А. Хоквингем (1959) и американцы Р. К. Боуз и Д. К. Рой-Чоудхури (1960) нашли большой класс кодов (коды БЧХ), исправляющих кратные ошибки. Американские исследователи И. С. Рид и Г. Соломон (1960) нашли связанный с кодами БЧХ класс кодов для недвоичных каналов.

В 1980 г. Хэмминг написал блестящий учебник “Теория кодирования и теория информации”, который в 1983 г. был переведен на русский язык. Эту книгу, как и другие его труды, отличает оригинальность постановки вопросов, популярность изложения, глубокое понимание практических задач, корректность и разумная степень строгости математической трактовки затронутых вопросов. Изложение материала построено таким образом, что читателю интуитивно понятно, почему справедлива та или иная теорема.

Ричард Хэмминг обладал широчайшей эрудицией. В сферу его научных интересов входил обширный круг математических и технических проблем. Он получил первоклассные результаты не только в теории кодирования, но и в ряде других областей науки.

В 1956 Хэмминг, работая над созданием одного из первых компьютеров IBM 650, предложил язык программирования высокого уровня, который применяется и сегодня. Интересны его исследования в области численных методов решения разного рода прикладных математических задач. Он создал новые методы численной интеграции дифференциальных уравнений и спектрального анализа и предложил использовать для сглаживания данных при спектральном анализе окно Хэмминга, позволяющее осуществлять их предварительную эффективную фильтрацию, избавляясь от ошибок измерений.

Хэмминг прославился не только как ученый, но и как выдающийся педагог. Выражаясь словами Бердяева, вынесенными в эпиграф к этому очерку, он “каждое мгновение жизни проявлял творчество и изобретательность”. С 1962 по 1997 гг. им написано восемь книг по прикладным численным методам анализа, цифровым фильтрам, теории кодирования и теории информации, теории вероятностей и математической статистике. В книгах проявилось большое научное и педагогическое дарование автора, и они вследствие их изумительной ясности пользовались огромной популярностью. Три его труда (по численным методам анализа, цифровым фильтрам и по теории кодирования и теории информации) были изданы в России.

Создавая эти замечательные книги, Хэмминг видел свою задачу не только в том, чтобы специалисты получили глубокие знания, он стремился к тому, чтобы они почувствовали сам дух науки. Его девизом было: “Цель расчётов – не числа, а понимание”.

В своей последней весьма интересной книге “Искусство научного исследования и изобретения: учиться изучать (“The Art of Doing Science and Engineering: Learning to Learn”), изданной в 1997, Хэмминг изложил философские взгляды на природу и принципы научного творчества.

Источники: 

1. Быховский Марк. Ричард Хэмминг и начало теории кодирования  // PC Week/RE № 21 от 11.06.2002, стр. 29.

Последнее обновление страницы   23.10.04 15:16:20